这篇博客主要是针对2019主要介绍的是第十六届(2019)全国研究生数学建模竞赛(NPMCM)试题B题：天文导航中的星图识别，这里我下载了5篇优秀论文，以及优秀的答辩现场录像，在这篇博客中，我将选取B19102880053提到的基于角距传统算法进行复现。

此赛题提供的4908个导航星表数据是.mat文件，因此将使用MATLAB进行代码编写。

  • 1、星表数据处理

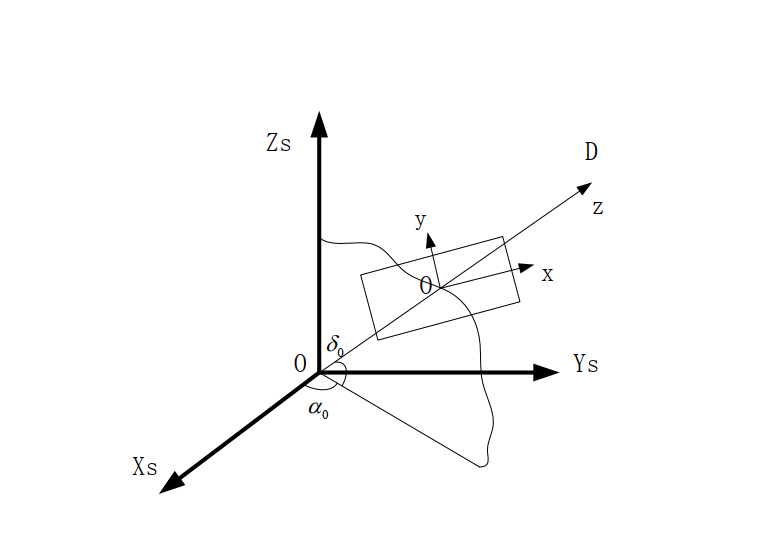
    首先将星表数据的天球坐标系下的赤经、赤纬转为直角坐标系下的x/y/z轴的值，利用公式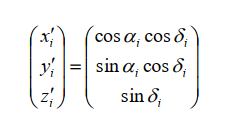

    得到

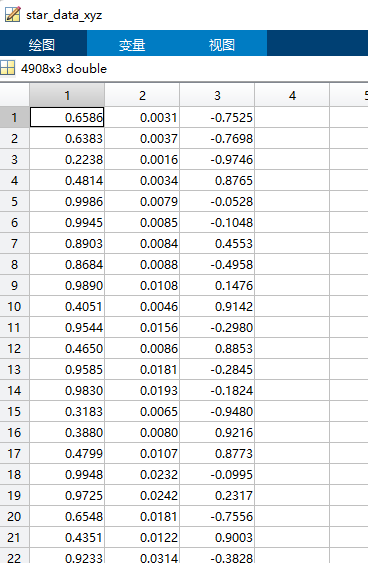
  • 2、准备库矩阵和星图矩阵

    • 式6-1导航星角距库比较好理解，我将其化成度数，得到：

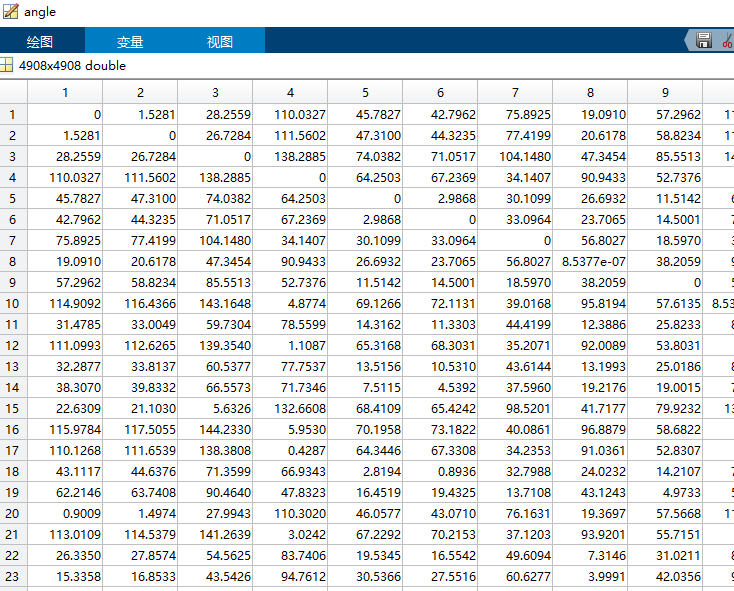
    • 而式6-2某星图角距矩阵，文中作者提到选取导航星方式，但不妨以任意星，例如表中顺序来求。在此我选取第一个星A01作为基准星，求解与其他星的角距，但在此我去除了与本身星的角距（因其为0），得到如下角距：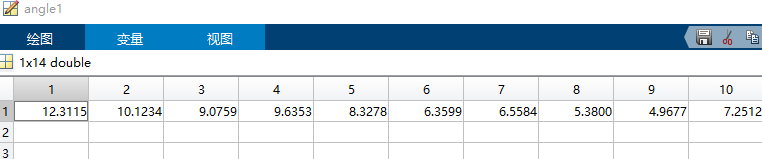

  • 3、算法描述

    （其实在此我理解错了，怪不得我运行了这么长时间，先说一下我的理解的算法，是没有优化的算法，在于最后一步还进行遍历循环。）

    取星图角距矩阵第i(i=1)个元素与导航星角距矩阵第j(j=1)列的元素依次匹配，若匹配到角距相等或近似的元素，判断矩阵第i(i=1)个元素数值加 1；

    main3.m

    if (   length(find(abs(angle(:,j)-angle1(i)) < 0.1  ) % 这里的0.1是匹配到角距的判定
    	panduan(j) = panduan(j)+ 1 ;
    end

    取星图角距矩阵第i （ i= 2,3,…,n）个元素，重复上一步操作； （该步完成后，若导航星就是第j列，则判断矩阵会加很多个1；）

    for i = 1:size(angle1,2) 
    	if (   length(find(abs(angle(:,j)-angle1(i))< 0.1  )
    		panduan(j) = panduan(j)+ 1 ;
    	end
    end

    若星图矩阵所有元素均完成匹配，则取导航星矩阵第 j （ j = 2,3,…,4908）列元素重复上两步操作； 

    for j = 1:4908
    	for i = 1:size(angle1,2) 
    		if (   length(find(abs(angle(:,j)-angle1(i))< 0.1     )
    			panduan(j) = panduan(j)+ 1 ;
    		end
    	end
    end

    取判断矩阵最大元素所在列（记为 x ）作为基准星编号 x ；

    （关于0.1的设置，假设其为a，我希望采用智能化判断，即当判断矩阵的最大的一个值不大于最大的值的2倍时，差距a减半，继续判断，直到第一个值大于第二个值，即能够明显判断出差异和保证准确性时，判断截止）

    for delta=1:10 
           panduan = zeros(1,4908);
           for j = 1:4908
               for i = 1:size(angle1,2) 
                   if (   length(find(abs(angle(:,j)-angle1(i))< (2^(-delta))))     )
                       panduan(j) = panduan(j)+ 1 ;
                   end
               end
           end
           [max,I ] = maxk(panduan,5)
           if( max(1) > max(2)*2 )
               newNewMatrix(ii,4)=I(1); 
               break;
           end
       end

    继续匹配导航星矩阵第 x 列，确定星图其他恒星编号 。（其实我的理解的差别在这，作者由基准星的列直接判断其他星，而笨拙的方法是遍历其他基准星，若采用笨拙的方法，星图1将耗时60s，若不遍历，则耗时6s左右，若设定固定0.1差距，则耗时1s左右）

    for ii = 1:size(newNewMatrix,1)

        angle1 = real(acosd(newNewMatrix(ii,1:3) * newNewMatrix(:,1:3).'));
        angle1(find(angle1==0))=[];
        
        for delta=1:10 
            panduan = zeros(1,4908);
            for j = 1:4908
                for i = 1:size(angle1,2) 
                    if (   length(find(abs(angle(:,j)-angle1(i))< (2^(-delta))))     )
                        panduan(j) = panduan(j)+ 1 ;
                    end
                end
            end
            [max,I ] = maxk(panduan,5)
            if( max(1) > max(2)*2 )
                newNewMatrix(ii,4)=I(1); 
                break;
            end
        end
    end

该方法在识别星图1和星图2的时候有较好的效果。但在识别星图3的时候，由于存在的星较少，星之间相距较近 的条件比较苛刻，判断条件需要优化，之前是判断最多的匹配个数大于次多的匹配个数的两倍，现在可能由于delta的缩放比例过大导致无法适应条件进行判断，因此需要修改delta的条件。

对于星图3只能识别出C05

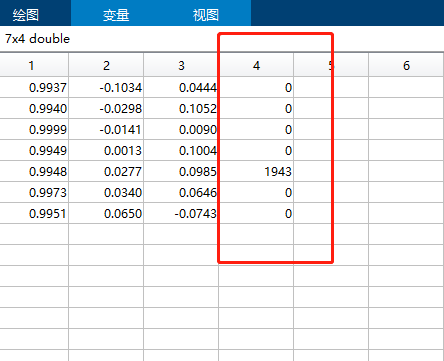
image-20220109105948234

通过对每一个星、每一种delta得出的前几匹配数可见，其实星图3是存在位置误差的，C02、C04、C06、C07存在较大误差。接着对星图4、5验证没问题，对于星图6部分有问题。

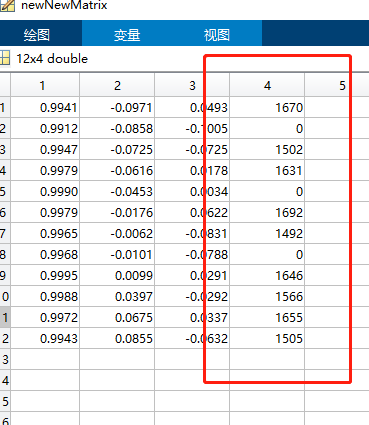
image-20220109105820180

接着识别星图7，总结当前代码为：

tic
clc;clear;close all;
load("附件2  简易星表.mat");

star_data_xyz(:,1) = cos(star_data(:,2) * pi / 180) .* cos(star_data(:,3) * pi / 180);
star_data_xyz(:,2) = sin(star_data(:,2) * pi / 180) .* cos(star_data(:,3) * pi / 180);
star_data_xyz(:,3) = sin(star_data(:,3) * pi / 180);

angle = real(acosd(star_data_xyz(:,1:3) * star_data_xyz(:,1:3).'));
panduan = zeros(1,4908);

h2 = 512/(tand(10));
A = xlsread('D:\文献\starimage\npmcm2019b\npmcm2019-B\附件3  8幅星图相关数据\xingtu07.xls') - 512;

for j = 1:size(A,1)
    l(j,1) = norm(A(j,:));
end

newMatrix= [repmat(h2,size(A,1),1),A];

for j = 1:size(newMatrix,1)
    ll(j,1) = norm(newMatrix(j,:));
end

newNewMatrix = newMatrix./ll;

for ii = 1:size(newNewMatrix,1)
% ii = 7;

    angle1 = real(acosd(newNewMatrix(ii,1:3) * newNewMatrix(:,1:3).'));
    angle1(find(angle1==0))=[];
    
    for delta=1:15 
        panduan = zeros(1,4908);
        for j = 1:4908
            for i = 1:size(angle1,2) 
                if (   length(find(abs(angle(:,j)-angle1(i))< (2^(-delta))))     )
%                 if (   length(find(abs(angle(:,j)-angle1(i))< 0.0001       ))     )
                    panduan(j) = panduan(j)+ 1 ;
                end
            end
        end
        [max,I ] = maxk(panduan,5);
        if( max(1) == 1 )
            break;
        end
        if( max(1) > max(2)*2 )
            newNewMatrix(ii,4)=I(1); 
            break;
        end
    end
end

toc
disp(['运行时间: ',num2str(toc)]);

对于星图7，识别41个星耗时573秒，判断结果全对。

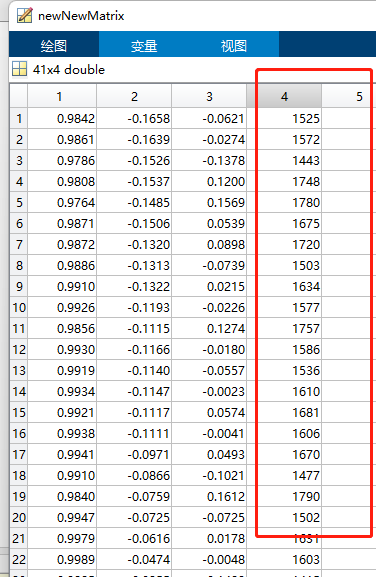
image-20220109111249906

对于星图8，识别29个星耗时319秒，判断结果全对。

到此为止，我描述了我的 遍历每个星作为基准星的方法，对于星图124578没问题，对于星图36存在找不全的情况。

回到使用基准星的方法来看，使用基准星确实能加速识别过程，例如识别20个星，只需要识别出一个星，再找到对应的矩阵即可。并且使用基准星可以避免找不到星的情况。

如何挑选这个基准星呢？ 文中也没给出较好的计算方法。

对于一个基准星来说或许不可靠，能否有一个初步方法筛选出相对可靠的若干基准星？ 发现还是一个基准星来的快一些

得到若干基准星后，得到其他星之后是否有一个验证过程？ 当选择用一个基准星的时候其实已经进行了一轮验证。

总结上面的实验可得，后续的改进优化需要先快速算出基准星，再由基准星得到其他星，最后进行验证。

基准星一定是相对最可靠的，遍历还是需要遍历，但遍历深度不可太深。

% 来自B19102880053.pdf的角距矩阵匹配模型。
% 找到一个基准星，然后找到其他星
% main4.m

tic
clc;clear;close all;
load("附件2  简易星表.mat");

star_data_xyz(:,1) = cos(star_data(:,2) * pi / 180) .* cos(star_data(:,3) * pi / 180);
star_data_xyz(:,2) = sin(star_data(:,2) * pi / 180) .* cos(star_data(:,3) * pi / 180);
star_data_xyz(:,3) = sin(star_data(:,3) * pi / 180);

angle = real(acosd(star_data_xyz(:,1:3) * star_data_xyz(:,1:3).'));
panduan = zeros(1,4908);

h2 = 256/(tand(6));
A = xlsread('D:\文献\starimage\npmcm2019b\npmcm2019-B\附件3  8幅星图相关数据\xingtu03.xls') - 256;



newMatrix= [repmat(h2,size(A,1),1),A];
for j = 1:size(newMatrix,1)
    ll(j,1) = norm(newMatrix(j,:));
end
newNewMatrix = newMatrix./ll;

flag = 0;
for delta=5:15 

    for ii = 1:size(newNewMatrix,1)
        panduan = zeros(1,4908);
        angle1 = real(acosd(newNewMatrix(ii,1:3) * newNewMatrix(:,1:3).'));
        angle1(find(angle1==0))=[];
        
        for j = 1:4908
            for i = 1:size(newNewMatrix,1)-1
                if (   length(find(abs(angle(:,j)-angle1(i))< (2^(-delta))))     )
                    panduan(j) = panduan(j)+ 1 ;
                end
            end
        end

        [max,I ] = maxk(panduan,2);
        if( (max(1) == 1) || (max(1) == 0) )%将不讨论这个星
            break;
        end
        if( max(1) >= max(2)+2 )
            newNewMatrix(ii,4)=I(1); 
            flag=1;
            break;
        end

    end
    if (flag ==1 )
        break;
    end
end

angle1 = real(acosd(newNewMatrix(ii,1:3) * newNewMatrix(:,1:3).'));

for i = 1:size(angle1,2)

    A = abs(    angle(:,newNewMatrix(ii,4)) -angle1(i)    );
    [minvalue,I] = min(A);
    newNewMatrix(i,5) = I(1);

end




toc
disp(['运行时间: ',num2str(toc)]);

星图全遍历91s、找到一组基准星57s，找到一个基准星43s，最快设置delta 2.23s，

在此我将计算每个星图的指向参数。

结果可以参考003.pdf，以下为main4.m的结果，左侧为基准星

星图1结果：2s多

0 1670
0 1477
1502 1502
0 1631
0 1603
0 1453
0 1432
0 1492
0 1488 与053.pdf不同
0 1648
0 1646
0 1566
0 1688
0 1655
0 1505

星图2结果：1s多

0 518
472 472
0 537
0 428
0 491
0 469
0 482
0 503
0 478
0 499
0 547
0 460
0 507
0 556
0 447
0 479

星图3结果：15s多

0 1864
0 1942
0 1825
0 1941
1943 1943 与053.pdf不同 可以确定不需要参考053答案。
0 1900
0 1722

星图4结果：4s 与003.pdf相同

0 3249
0 3346
0 3364
0 3275
0 3421
0 3319
3283 3283
0 3370
0 3265
0 3261
0 3321
0 3309

星图5：5.3s 与003.pdf相同

0 1230
0 1150
0 1017
1033 1033
0 1014
0 1223
0 1008
0 1208
0 1201

星图6： 11s

0 1670
0 1675 003.pdf为1477
0 1502
0 1631
0 1655 003.pdf为1603
0 1692
0 1492
0 1576 003.pdf为1488
1646 1646
0 1566
0 1655
0 1505

星图7:2.1s

1525 1525
0 1572
0 1443
0 1748
0 1780
0 1675
0 1720
0 1503
0 1634
0 1577
0 1757
0 1586
0 1536
0 1610
0 1681
0 1606
0 1670
0 1477
0 1790
0 1502
0 1631
0 1603
0 1415
0 1692
0 1453
0 1432
0 1492
0 1488
0 1648
0 1646
0 1566
0 1688
0 1655
0 1505
0 1373
0 1576
0 1545
0 1424
0 1375
0 1825
0 1401

星图8为1.6s：

1572 1572
0 1387
0 1675
0 1634
0 1586
0 1610
0 1354
0 1681
0 1606
0 1670
0 1390
0 1502
0 1631
0 1603
0 1692
0 1432
0 1488
0 1648
0 1646
0 1566
0 1688
0 1359
0 1505
0 1373
0 1576
0 1424
0 1375
0 1401
0 1385

以main4.m的结果来看，仅星图6有差，后续再验证。