冲毕业第六七八周记录
一些相关的文章
Distribute points evenly on a unit hemisphere
https://zhuanlan.zhihu.com/p/25998937
但并不适用于矩形上选择
突然发现一个很大的问题,我不能使用该方法来寻找星点,因为这种均匀分布是星点之间的角距的均匀分布,在观测时高度越高观测点越少,在高度低的地方观测点较多,其实并不适用于机架的校正。机架的校正应该按照经纬度网格来均匀选取。

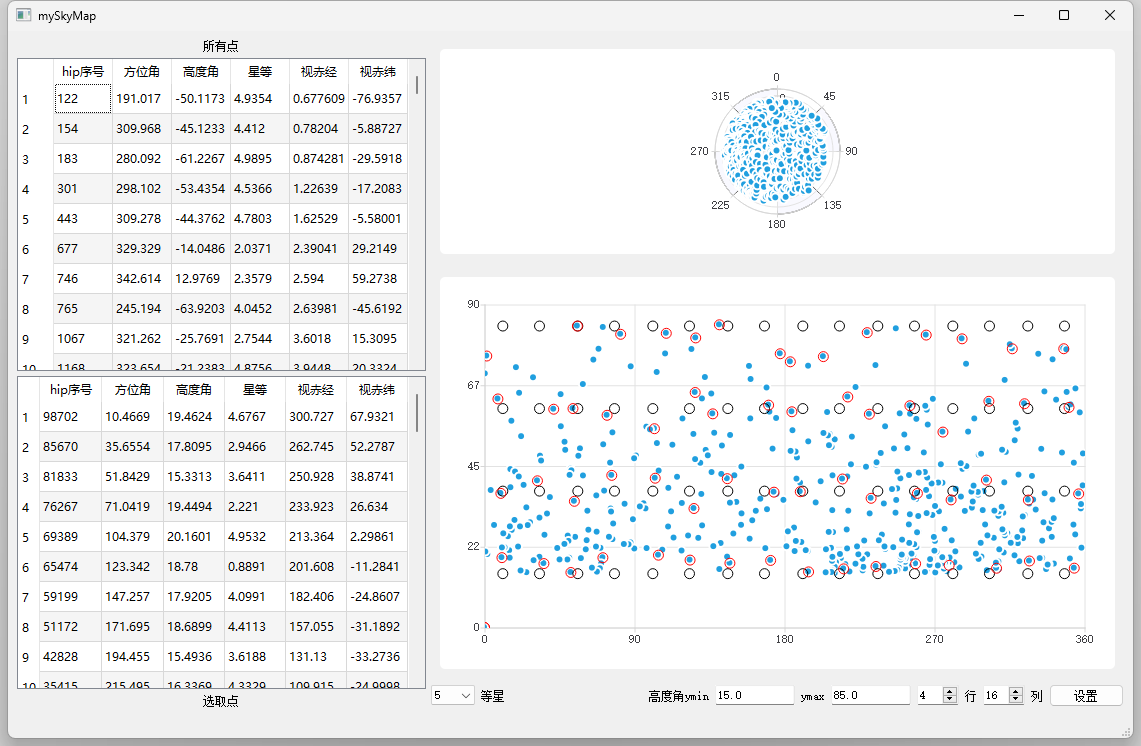
那么其实就可以将头顶的天区展开为一个矩形,方位和高度为边的矩形,研究在矩形上的二维均匀分布。

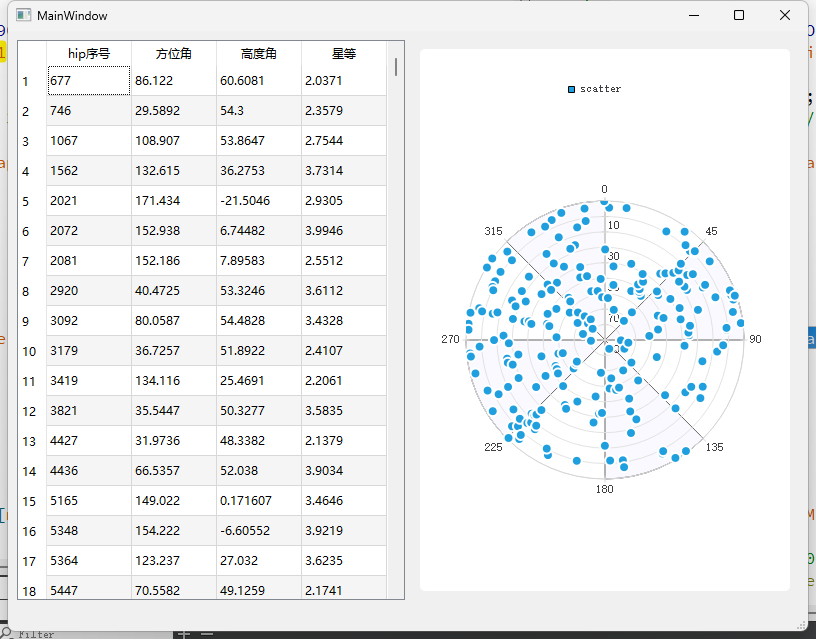
浅画一下二维的高度方位图(5等星
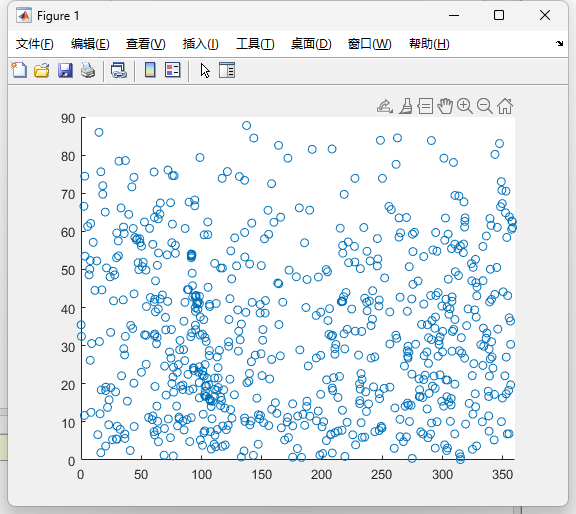
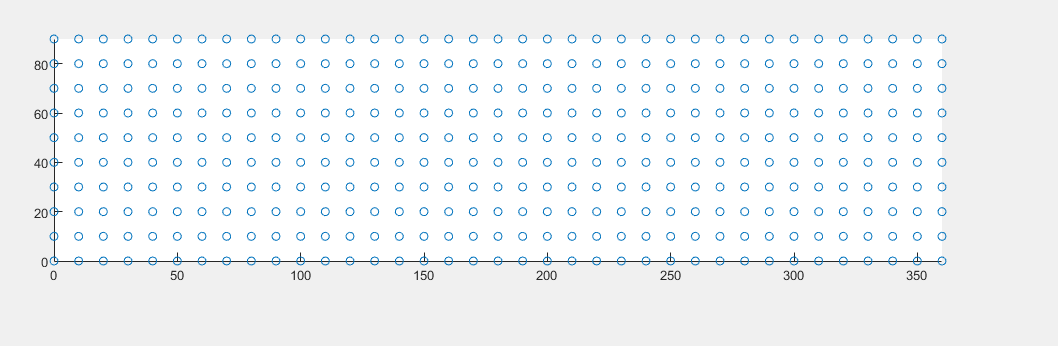
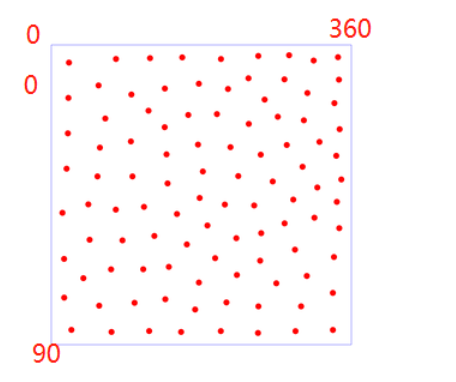
论文
Vedder, J.D.: ‘Star trackers, star catalog, and attitude determination: probabilistic aspects of system design’, J. Guid. Control Dyn., 1993, 16, (3), pp. 499–504
专利 《用于星敏感器的筛选导航星的方法》
2004

在Stack Overflow中找到了我想问问题的答案
通常在统计学中,我们需要了解给定的样本是否来自特定的分布,最常见的是正态分布(或高斯分布)。为此,我们有所谓的正态性检验,如夏皮罗-威尔克,安德森-达林或Kolmogorov-Smirnov检验。
它们都测量样本来自正态分布的可能性有多大,并有相关的p值来支持这种测量。
就是KS检验。Kolmogorov-Smirnov test是一个有用的非参数(nonparmetric)假设检验,主要是用来检验一组样本是否来自于某个概率分布(one-sample K-S test),或者比较两组样本的分布是否相同(two-sample K-S test)。
ks检验返回两个值,pvalue是越高越好,统计量D-statistic越低越好
值的解释
https://en.m.wikipedia.org/wiki/Kolmogorov%E2%80%93Smirnov_test
D 统计量是两个样本的 CDF 之间的绝对最大距离(最大值)。这个数字越接近于0,这两个样本就越有可能来自同一个分布。
K-s 检验返回的 p 值与其他 p 值具有相同的解释。如果 p 值小于你的显著性水平,那么你就拒绝了两个样本来自同一个分布的无效假设。如果您对该过程感兴趣,可以在线找到将 D 统计量转换为 p 值的表。
最终返回的结果,p-value=4.7405805465370525e-159,比指定的显著水平(假设为5%)小,则我们完全可以拒绝假设:beta和norm不服从同一分布。
学习一下ks检验 柯尔莫哥洛夫-斯米尔诺夫检验(英语:Kolmogorov-Smirnov test,简称K-S test),是一种基于累计分布函数的非参数检验,用以检验两个经验分布是否不同或一个经验分布与另一个理想分布是否不同。

https://zhuanlan.zhihu.com/p/292678346
α是置信系数
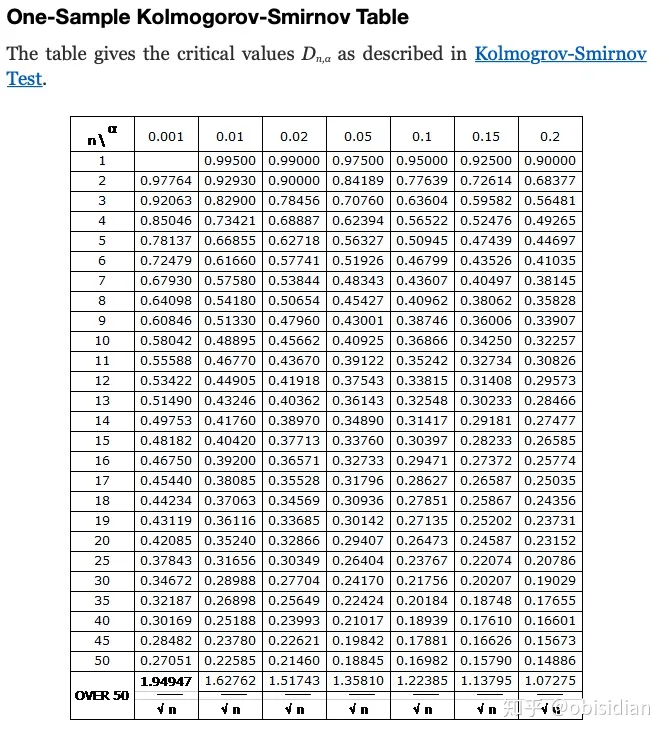
https://zhuanlan.zhihu.com/p/26477641
from scipy.stats import ks_2samp |
KstestResult(statistic=0.35803634777692694, pvalue=0.11834016917515)
用一种简单的方式,我们可以将2样本检验的KS统计量D 定义为每个样本的cdf(累积分布函数)之间的最大距离,cdf 累计分布函数 https://towardsdatascience.com/comparing-sample-distributions-with-the-kolmogorov-smirnov-ks-test-a2292ad6fee5
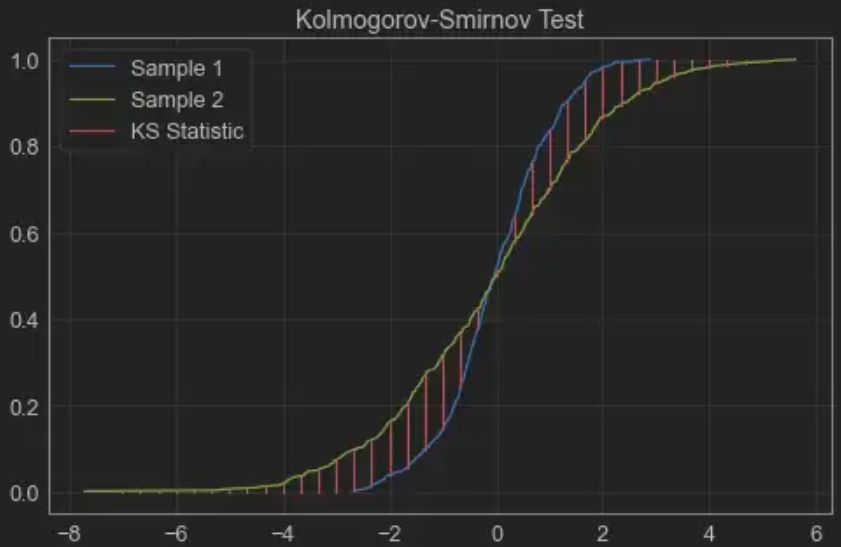
from scipy.stats import kstest |
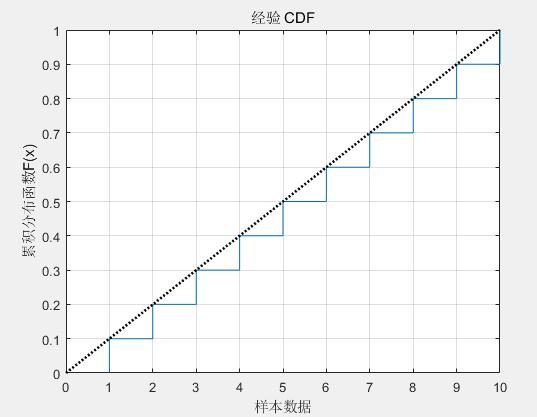
clc;clear;close all;
x = [1,2,3,4,5,6,7,8,9,10];
pd2 = makedist('Uniform','lower',0,'upper',10); % Uniform distribution with a = -2 and b = 2
t = 0:.01:10;
cdf2 = cdf(pd2, t);
h1 = cdfplot(x);
hold on
plot(t,cdf2,'k:','LineWidth',2);
xlabel('样本数据');
ylabel('累积分布函数F(x)');
clc;clear;close all; |
试试实时方位数据
from scipy.stats import kstest |
KstestResult(statistic=0.06621370056497172, pvalue=0.0038362399448040162)
实验感觉有问题 https://bbs.pinggu.org/thread-2983774-1-1.html
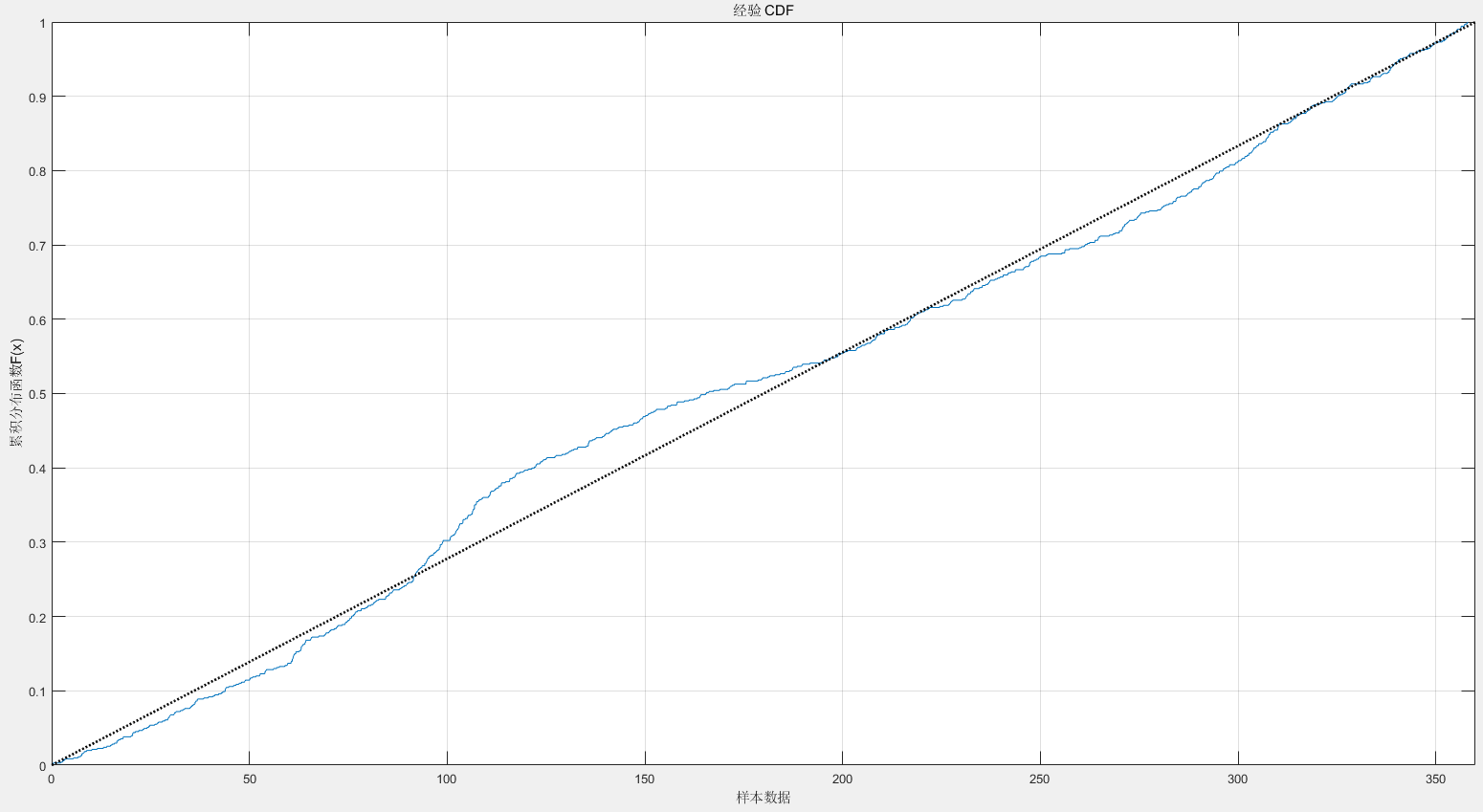
clc;clear;close all; |
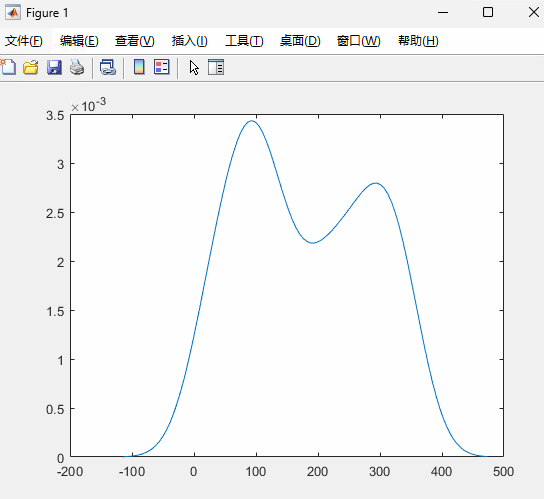
ks检验还是到此为止了,毕竟还只是个检验方法,不算指标
检验数据是否服从指定分布的方法有
https://blog.csdn.net/Datawhale/article/details/120558925
可知 KS检验的灵敏度没有相应的检验来的高
在该文中提到KL 散度是一种衡量两个概率分布的匹配程度的指标,两个分布差异越大,KL散度越大。KL越小越接近。
有人会把KL散度认为是一种距离指标,然而,KL散度不能用来衡量两个分布的距离。其原因在于KL散度不是对称的。举例来说,如果用观测分布来近似二项分布,其KL散度为
https://zhuanlan.zhihu.com/p/153492607
感觉不太合适,所以作罢
https://blog.csdn.net/qq_45654781/article/details/126862808
计算 Kozachenko-Leonenko的k最近邻估计熵
https://github.com/paulbrodersen/entropy_estimators
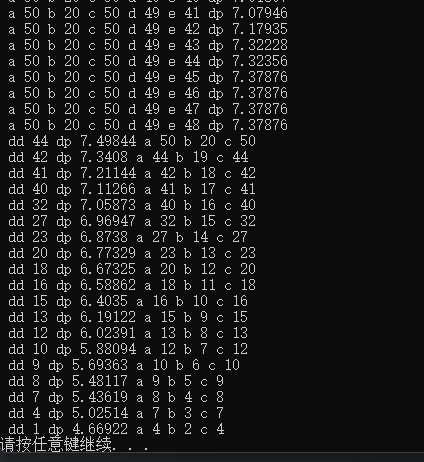
4等星 214个选20个
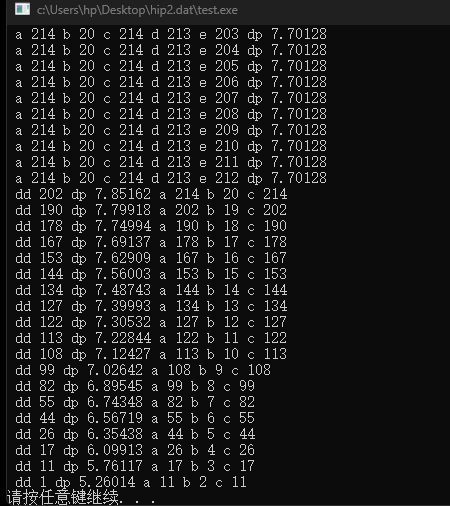
from scipy.special import gamma, digamma |
运算时间很慢
用c++写dp(这个dp还没考虑球体的循环问题)
|
采用模拟退火进行加速运算
b站教程不错
选用第三个例题《书店买书》的案例
https://mp.weixin.qq.com/s/001Klrt7jjf8s5rI3py7Yg
clear all;close all; clc; |
初始方案是:
[1 12 15 50 60 89 98 99 106 124 126 131 133 134 150 151 165 202 206 207]
此时最优值是:
46.3648
最佳的方案是:
[7 15 21 28 42 53 60 78 96 105 109 118 127 137 150 166 176 190 203 214]
此时最优值是:
93.4483
初始点:
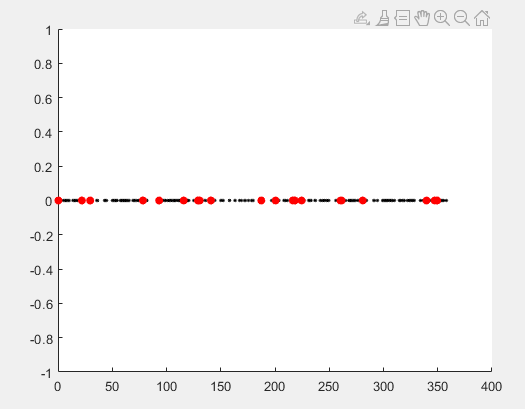
优化方案:
%% 模拟退火解决书店买书问题 % 466 |
用py验证一下
改变一下distance的定义,由于要循环
def get_h(x, k=1, norm='max', min_dist=0.): |
初始方案是:
[26 27 36 38 52 64 69 77 86 102 132 149 150 154 156 157 173 187 199 201]
此时最优值是:
26.7911
最佳的方案是:
[5 12 19 27 44 57 87 103 110 120 126 132 138 147 152 165 172 188 198 210]
此时最优值是:
70.6790
历时 3.124118 秒。
迭代计算只需要计算那改变的6个点,试试直接计算h0 看时间会多慢
%% 模拟退火解决书店买书问题 % 466 |
历时 3.305654 秒。
但耗时也不多
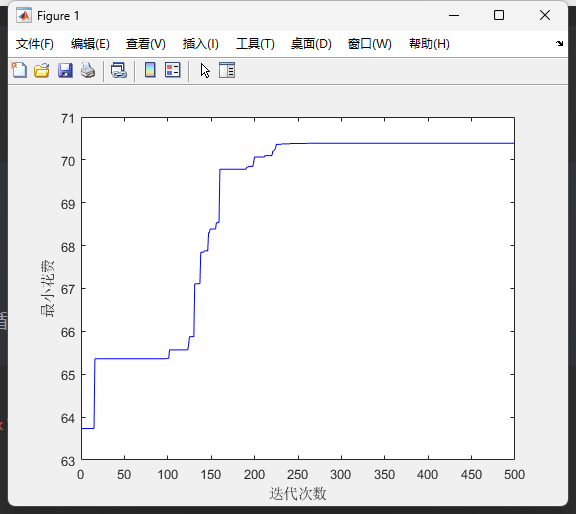
但增加迭代次数
maxgen = 1000; % 最大迭代次数
Lk = 1000; % 每个温度下的迭代次数
初始方案是:
[10 26 35 62 76 77 91 120 129 130 141 151 163 166 176 180 182 208 209 214]
此时最优值是:
43.8157
最佳的方案是:
[10 17 23 40 53 67 90 105 110 120 126 131 138 148 153 166 172 188 200 214]
此时最优值是:
70.7798
历时 31.648947 秒。
而只用6个点的数据
历时 29.961089 秒。
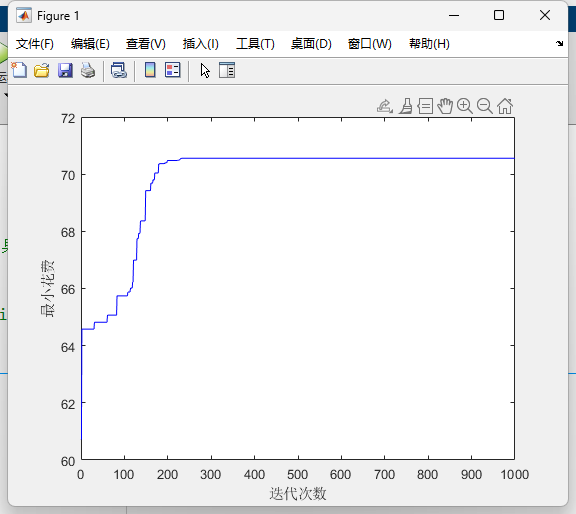
708个点选50个点也只需要4s
初始方案是:
[7 32 33 83 98 103 106 113 139 152 161 164 171 201 220 229 235 257 280 298 299 319 332 349 352 355 360 365 373 393 401 407 434 450 455 470 479 506 508 531 540 548 565 566 589 603 640 679 689 707]
此时最优值是:
73.5312
最佳的方案是:
[12 26 39 52 64 74 82 93 119 132 151 166 184 208 230 255 271 285 296 305 320 329 342 350 359 367 379 389 406 427 439 455 466 474 486 492 503 519 530 544 561 577 598 615 630 639 651 672 686 708]
此时最优值是:
130.3724
历时 4.013932 秒。
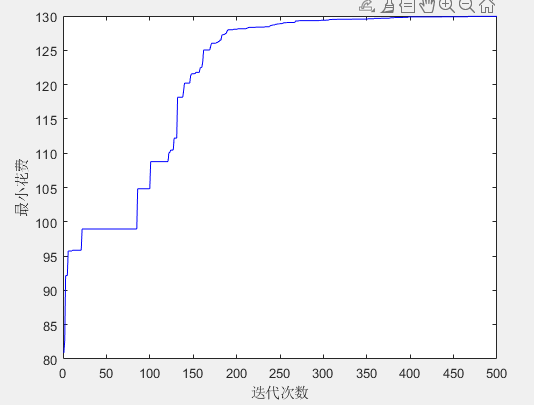
绝对完美的20个点是怎么样的
K-L estimator: 71.67038
50个点则是
K-L estimator: 133.36141
研究一下归一化