冲毕业第五周记录
接下来将由已经处理过的j2000转为视赤经赤纬,再转为地平坐标 J2000_x_hor。
设定时间为2022.12.10. 20:00,儒略日为2459924,经纬度为合肥{31.8642, 117.287}
int main() |
算6.5等星也只需0.131s
2等星 46个星 当前时刻地平以上的有20个
3等星 165个星 当前时刻地平以上的有67个
4等星 480个星 当前时刻地平以上的有214个
5等星 1471个星 当前时刻地平以上的有708个
6等星 4559个星 当前时刻地平以上的有2219个
6.5等星 7982个星 当前时刻地平以上的有3933个
目前文件夹目录下有这些文件
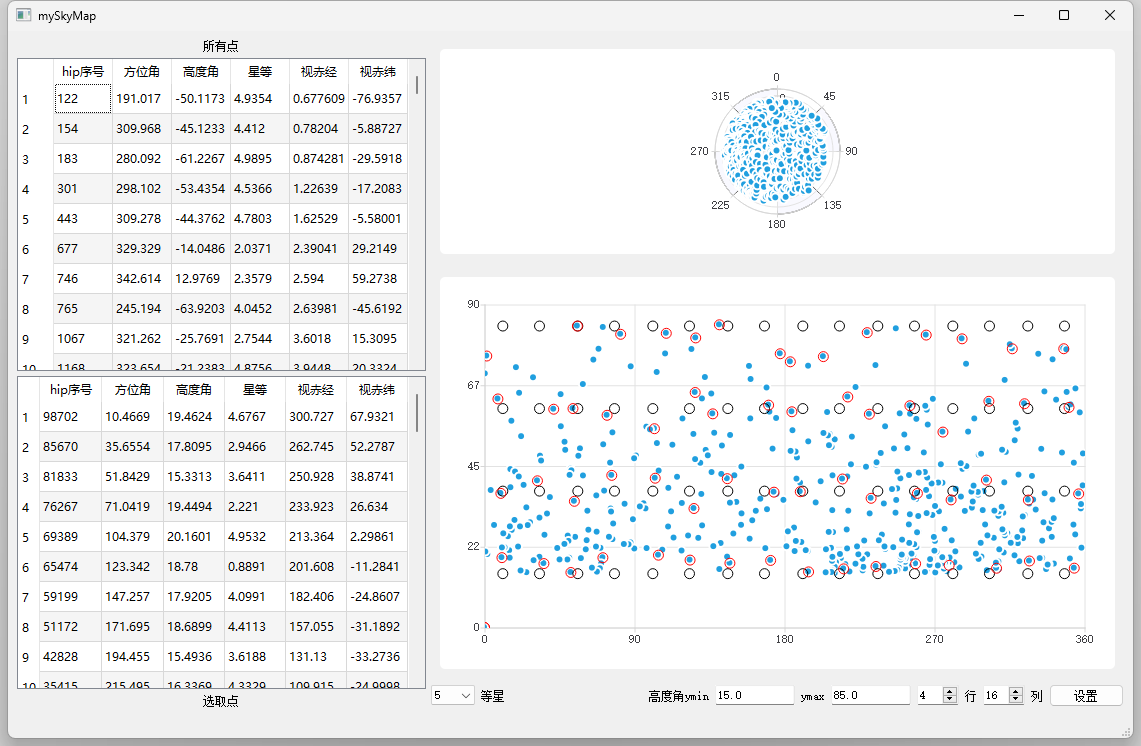
试试用qt显示
2等星
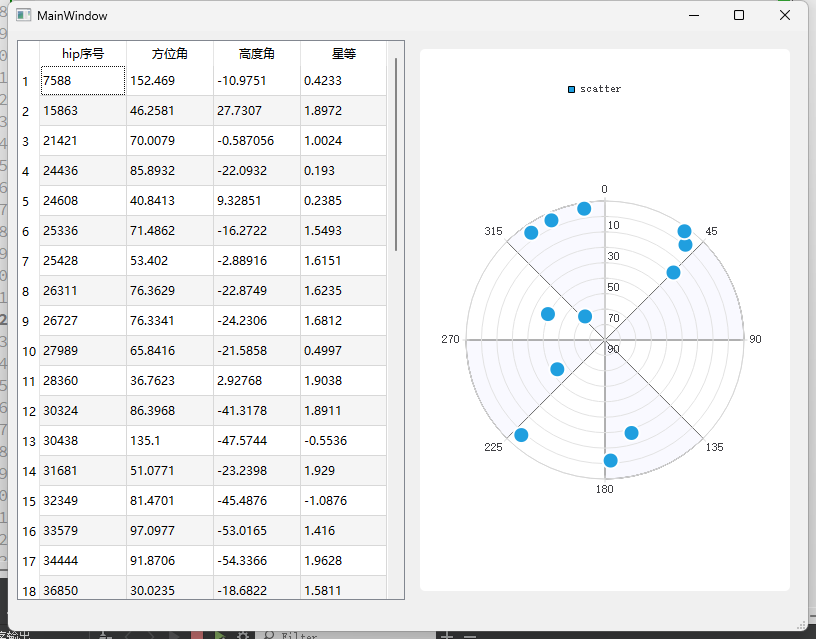
3等星
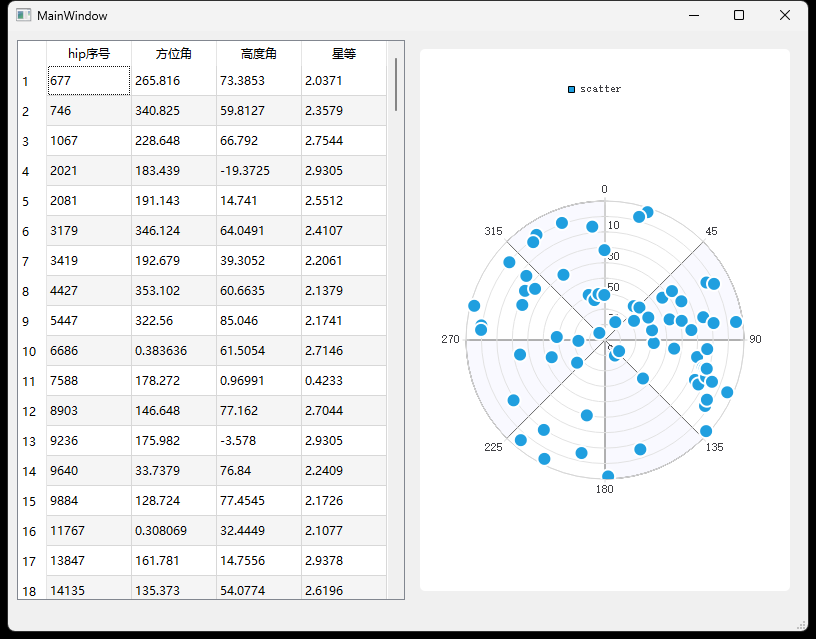
和下方对比 差不多

4等星
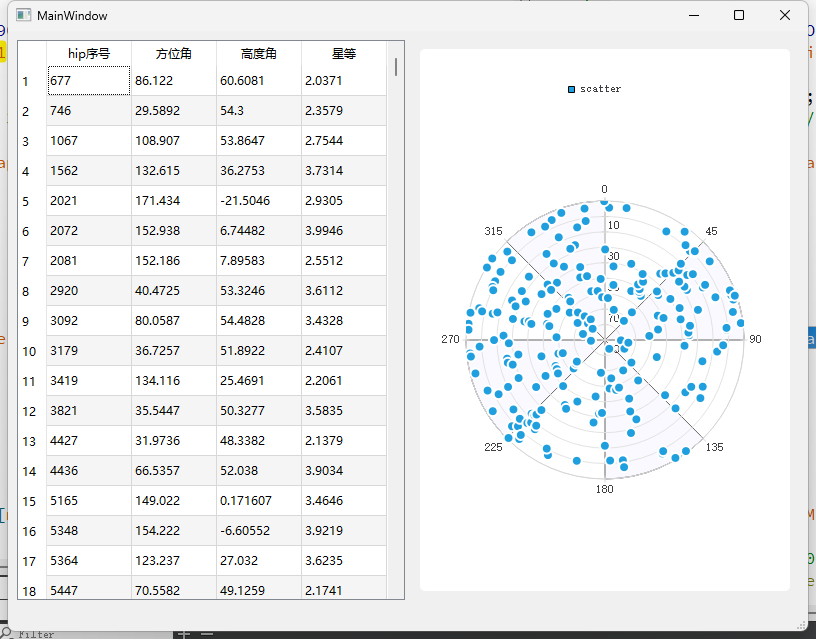
5等星
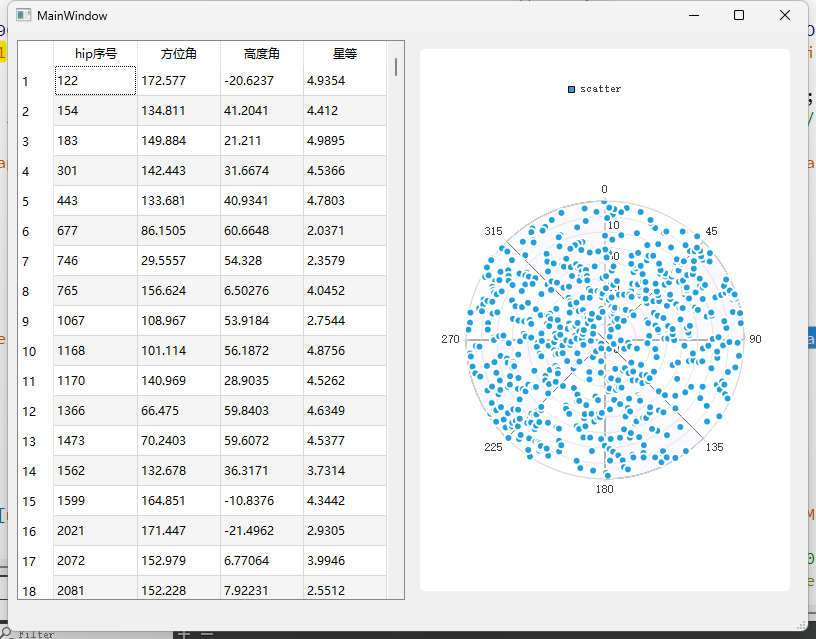
画到五等星还算较快,后面就很慢了 可以尝试用qpen来画
6等星

6.5等星
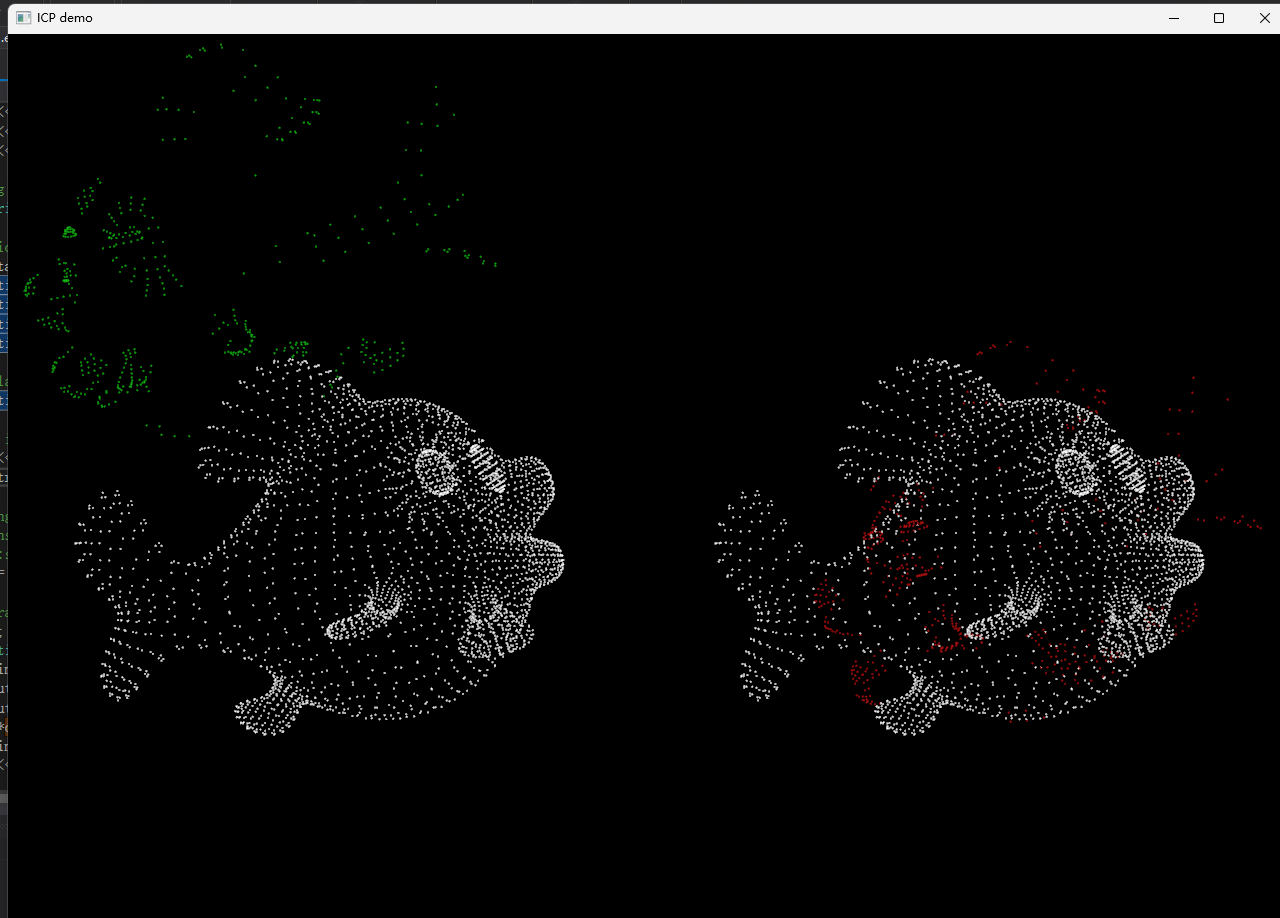
研究半圆球上的基准点的均匀性问题。还是很难实现,并且没有玻尔兹曼熵来作为参考,并且需要从天顶出发实时计算高度方位,当我望远镜转至该位置时,其他星点已离开螺旋基准点 最终形成的星点方位高度可能不均匀。
还是决定使用全天球的螺旋基准点,并且所有恒星围绕极轴转是一个天然的性质。并且可以一次选取 终生可用 任意时间可用。(但这也是错的想法,并不适用于地平式望远镜选星,只适用于星敏感器的导航星筛选。
将赤经赤纬坐标转为xyz轴
以右手坐标系为例,z轴指向北极点(高度角90度),x指向东(方位角90度),y指向北(方位角0度)
极坐标转xyz轴
double x = sin(ra) * sin(dec); |
|
测了一下正20面体的12个顶点的玻尔兹曼熵为0
0.850650808352040 -0.525731112119134 0 |
再测个足球 https://blog.sciencenet.cn/blog-2321-383987.html
.850651,0,2.327438; |
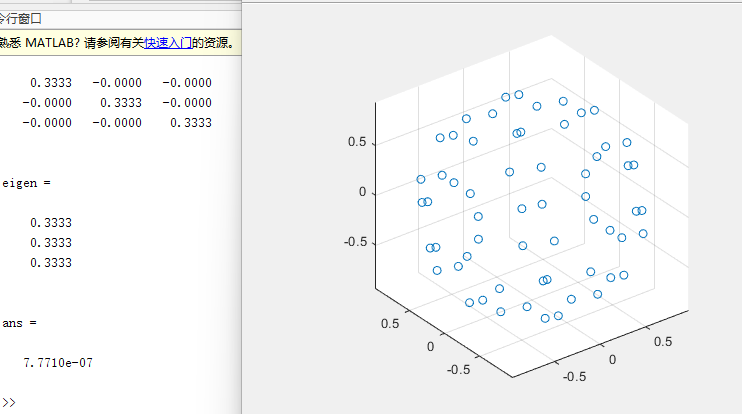
正四面体也同样
均匀分布没有得到很好的定义。从最严格的意义上来说,只有五个柏拉图立体(以及在一个大圆上所有节点间距相等的退化排列的无限族)可以符合条件: 每个节点有相同数量的邻居,在相同的距离,相同的间距。
突然发现一个很大的问题,我不能使用该方法来寻找星点,因为这种均匀分布是星点之间的角距的均匀分布,在观测时高度越高观测点越少,在高度低的地方观测点较多,其实并不适用于机架的校正。机架的校正应该按照经纬度网格来均匀选取。

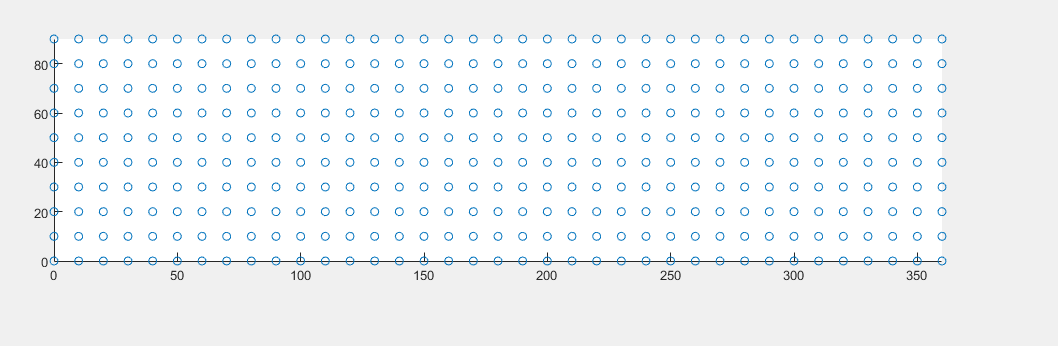
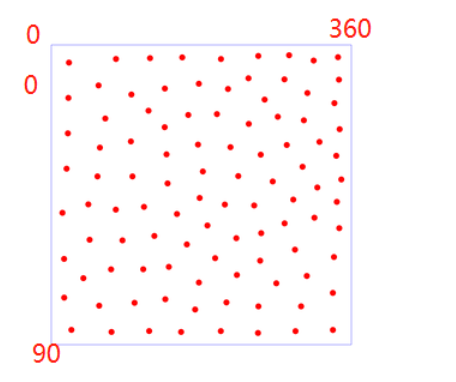
那么其实就可以将头顶的天区展开为一个矩形,方位和高度为边的矩形,研究在矩形上的二维均匀分布。

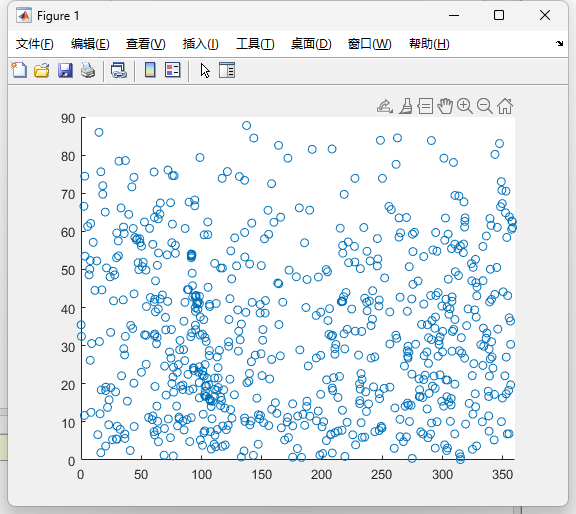
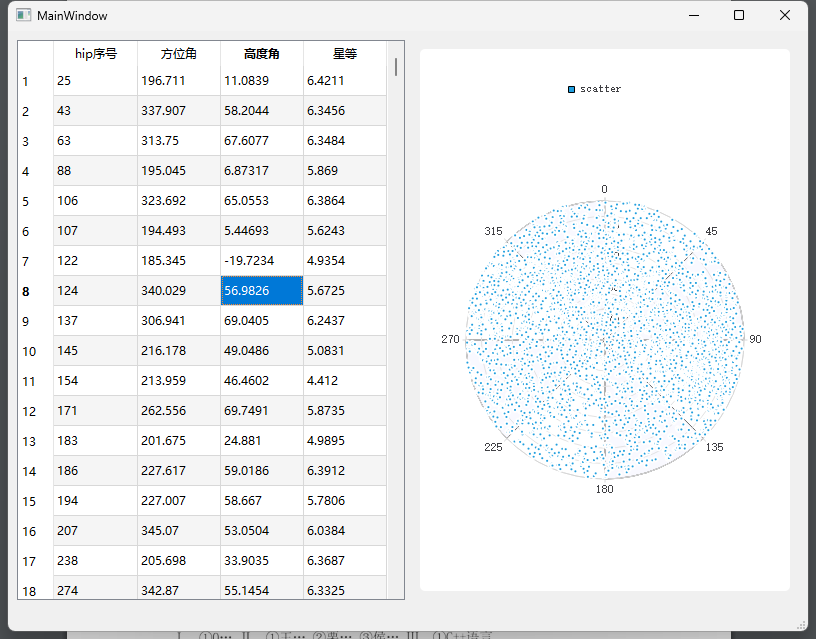
浅画一下二维的高度方位图(5等星