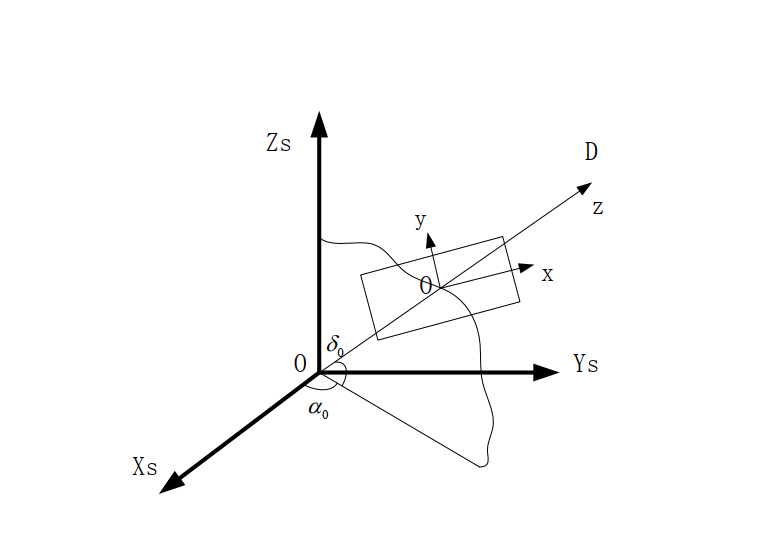
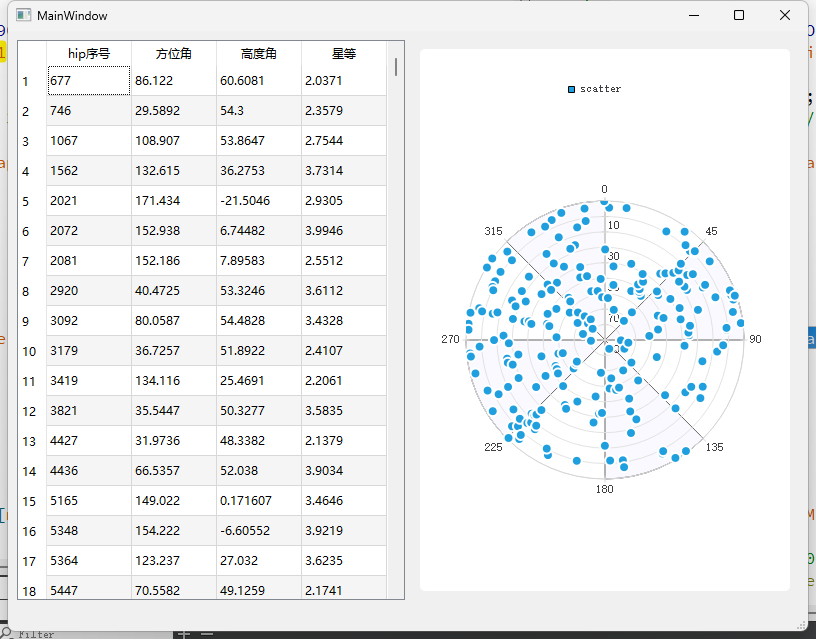
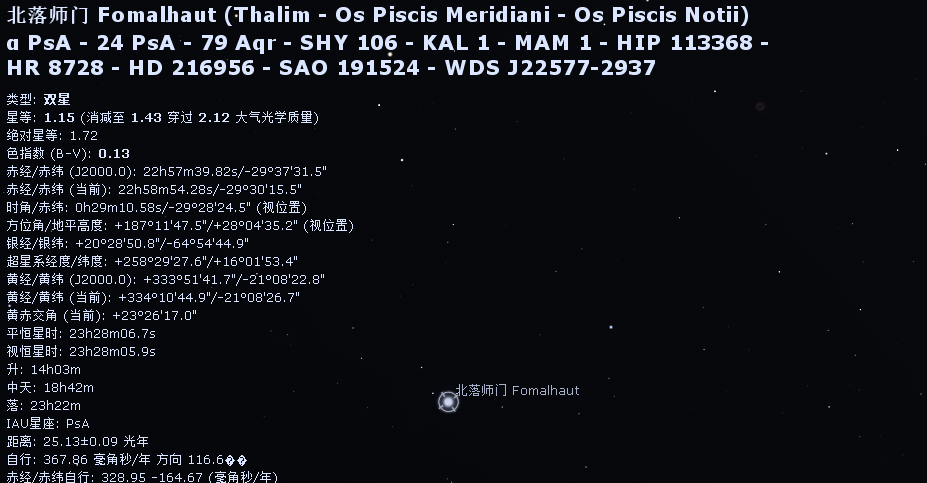
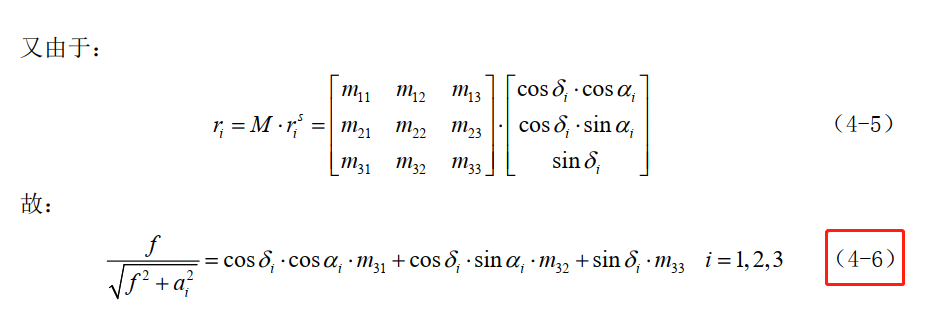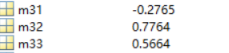根据 文章 B19910360003.pdf 中


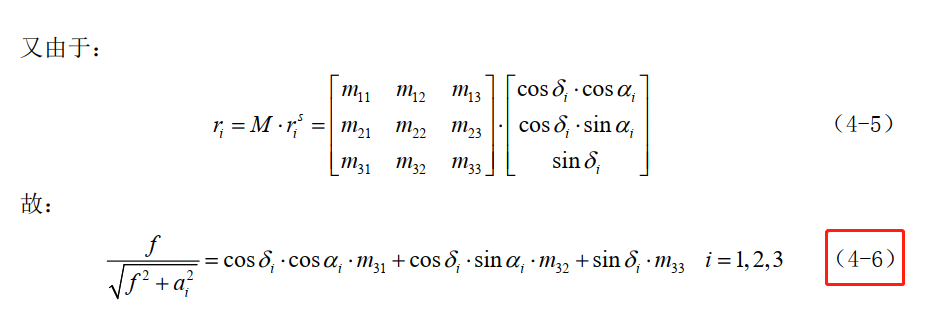
焦距f,即为相机坐标系下的投影中心到感光面的距离,即f = 256/(tand(6)); 单位位像素,与a保持一致。
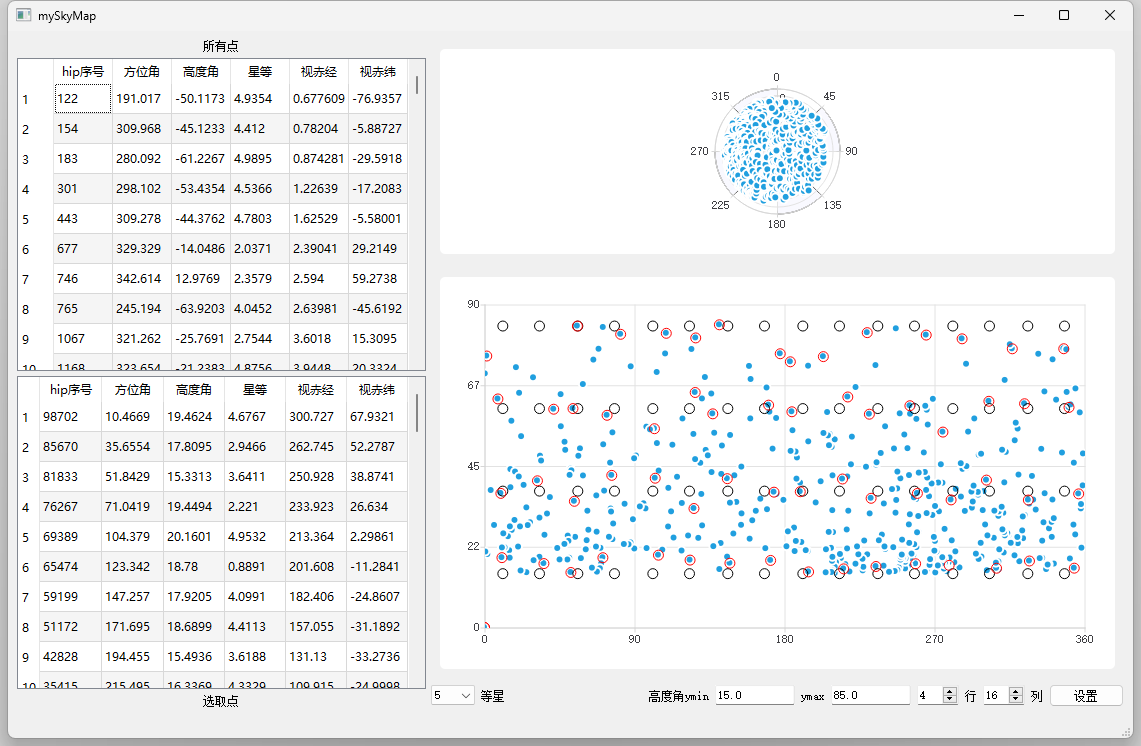
选前三点
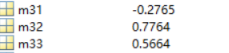
赤经赤纬为: 109.6002 34.5005


注意这里可能有2个解,在星图4中想了好几天。其中这里有错,赤经应该还可能等于360°-式。
经过研究,结合sin赤经的正负号表现,探究最终结论:
若tan赤经和cos赤经同号则为原式,否则为360°-式
if Res(2)/sqrt(1-Res(3)^2) > 0
[ acosd(Res(1)/sqrt(1-Res(3)^2)) , asind(Res(3)) ]
else
[ 360-acosd(Res(1)/sqrt(1-Res(3)^2)) , asind(Res(3)) ]
end
|

load("附件2 简易星表.mat");
f = 256/(tand(6));
A = xlsread('D:\文献\starimage\npmcm2019b\npmcm2019-B\附件3 8幅星图相关数据\xingtu01.xls') - 256;
newMatrix= [repmat(f,size(A,1),1),A];
for j = 1:size(newMatrix,1)
ll(j,1) = norm(newMatrix(j,:));
end
newNewMatrix = newMatrix./ll;
syms m31 m32 m33;
eqns = [
(f/(sqrt(f^2 + newMatrix(1,2)^2 + newMatrix(1,3)^2))) == cosd(star_data(1670,3))*cosd(star_data(1670,2))*m31 + cosd(star_data(1670,3))*sind(star_data(1670,2))*m32 + sind(star_data(1670,3))*m33,
(f/(sqrt(f^2 + newMatrix(2,2)^2 + newMatrix(2,3)^2))) == cosd(star_data(1477,3))*cosd(star_data(1477,2))*m31 + cosd(star_data(1477,3))*sind(star_data(1477,2))*m32 + sind(star_data(1477,3))*m33,
(f/(sqrt(f^2 + newMatrix(3,2)^2 + newMatrix(3,3)^2))) == cosd(star_data(1502,3))*cosd(star_data(1502,2))*m31 + cosd(star_data(1502,3))*sind(star_data(1502,2))*m32 + sind(star_data(1502,3))*m33
];
vars = [m31 m32 m33];
[m31, m32 m33 ] = solve(eqns, vars);
m31=double(m31);
m32=double(m32);
m33=double(m33);
if Res(2)/sqrt(1-Res(3)^2) > 0
[ acosd(Res(1)/sqrt(1-Res(3)^2)) , asind(Res(3)) ]
else
[ 360-acosd(Res(1)/sqrt(1-Res(3)^2)) , asind(Res(3)) ]
end
|
选全点:
方程组个数小于未知数个数,这种情形称为不定方程组,不定方程组一般有无穷个解。
方程个数大于未知数个数的方程组称为超定方程组,超定方程组一般无解。但是它存在最小二乘解。比较常见的情形是实际生活中,我们要测量某一组数据大小,为减小误差,必须重复测很多次,每测一次就是一组数据,这组数据就是一个超定方程组,它的最小二乘解就是误差最小的值。
算出最小二乘解是差不多的,赤经赤纬为:109.6000 34.5000
clc;clear;close all;
index = [1670
1477
1502
1631
1603
1453
1432
1492
1488
1648
1646
1566
1688
1655
1505];
load("附件2 简易星表.mat");
f = 256/(tand(6));
A = xlsread('D:\文献\starimage\npmcm2019b\npmcm2019-B\附件3 8幅星图相关数据\xingtu01.xls') - 256;
newMatrix= [repmat(f,size(A,1),1),A];
for j = 1:size(newMatrix,1)
ll(j,1) = norm(newMatrix(j,:));
end
newNewMatrix = newMatrix./ll;
A = [ cosd(star_data(index,3)).*cosd(star_data(index,2)) , cosd(star_data(index,3)).*sind(star_data(index,2)) , sind(star_data(index,3)) ];
Y = [ (f ./ (sqrt(f^2 + newMatrix(1:15,2).^2 + newMatrix(1:15,3).^2)) )];
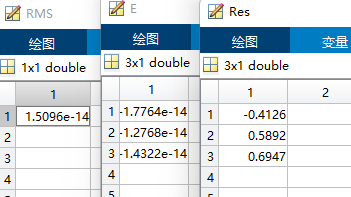
Res = inv(A'*A)*A'*Y;
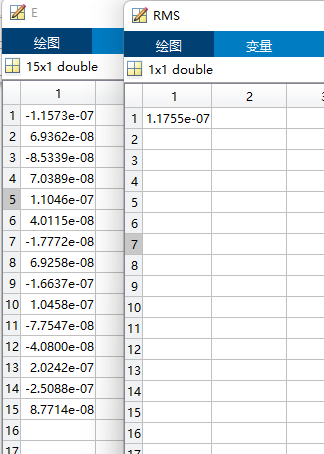
E = (A*Res - Y);
RMS = sqrt(mse(E))
|
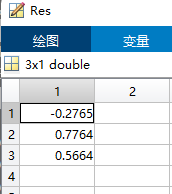
对于星图3
全点:赤经赤纬 124.9740 43.9973
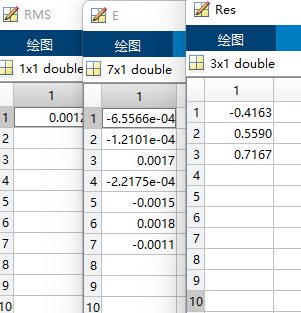
较为精准的3点:1825、1943、1722,赤经赤纬 125.0001 43.9999,和上对比,较为精准。
较为不精准的3点:1942、1941、1900,赤经赤纬 125.4325 44.2513,发现确实有较大偏差。